Astrophysics

Introduction

In order to study astronomy, it is important to understand how we are dealing with distances in the universe, because every branch of science has its own way of dealing with distances. The units of length differ based on what is convenient according to the system in which one is studying.

It might not come as a shock when I mention that there is an SI unit of length. That is meter. However, it would be ridiculous for an atomic or nuclear physicist to state spans in sense of meters or kilometers. Unlike in quantum systems, the universe is big, and astronomy is all about vastness. In astronomy we deal with distances in terms of the astronomical unit (AU), light years (ly) and parsec (pc).

– AU - average distance between earth and the sun. – Light year - the distance light travels in one year. – Parsec - 3.26 light years.

Astronomical unit

The astronomical unit is the average distance between earth and sun (average because earth orbits sun elliptically, not circularly). Why we use this particular measure to compare relative distances within the solar system is completely arbitrary, but useful. We could, of course, have used kilometers, but then we would need to constantly be operating with very large numbers.

[Missing image]

<figcaption>Distance between sun and planets in our solar system in astronomical units.</figcaption>

However, when moving out of the solar system, astronomical units start becoming inconveniently trivial again. That is when we start operating with light years and parsec.

Light year

It might be hard imagining how lingering one light year really is, and by just looking at the name, it might not seem that vast. It is, however, important to take into consideration that light is traveling with a really high velocity. In fact, at 300.000km per second. One year consists of 31.557.600 seconds, meaning that it is traveling almost 9.500.000.000.000km in one year. For comparison, light only needs 500 seconds to reach earth from the sun. We could say that the distance between sun and earth is 500 light seconds, but this distance we have already defined as 1 AU, and it might be best to stick with that.

We are rather using light years when studying distances outside of the solar system. The distance to our closest neighboring star (Proxima Centauri), for instance, is 4.3 light years away and the distance to the center of our galaxy is 26.000 light years.

Even though the astronomical unit and light years may appear to be satisfying astronomers’ needs for distance units, there is yet another one, seemingly akin to light years: Parsec. Although light years may be the most commonly known measure of cosmic distances, parsec is what is mainly used by astronomers, and is defined as 3.26 light years. This number may seem a bit arbitrary, but there is a logical explanation why and we are soon going to validate it. But first, it is crucial to understand how astronomers deal with angles when observing the universe.

Arcminutes and arcseconds

If you were to look at one degree of the sky, that would cover a huge region of space. Just imagine earth being divided into 360 equal parts and you could see everything within the region of space that was limited by the imaginary extended angular legs of that one individual degree. That is practically 1/360 of the universe, and that is a lot. Hence, when astronomers measure distances in angles, they do not, for practical reasons, deal with whole degrees. Instead, they divide them into even smaller segments called arcseconds and arcminutes.

In a complete circle with 360 degrees, each degree can be divided into 60 even angles in where each makes up one arcminute. Similarly, every arcminute can be divided into 60 arcseconds. In a circle there are 360 degrees, 21 600 arcminutes or 1 296 000 arcseconds. Now, we are ready to understand the definition of parsec.

Parsec and the parallax method

In astronomy, one of the oldest methods for determining distances to nearby stars is the parallax method. The main concept of this method is based upon the fact that earth is orbiting the sun, hence positioned differently relative to observed stars at different times of the year. If we study a particular star at one time and then, six months later do the exact same thing, the distance between the two positions of earth is 2 AU.

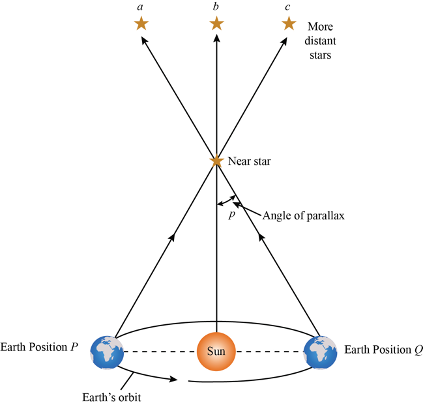
<figcaption>The Parallax Method</figcaption>

The parallax angle is the angle subtended the distance between earth at time₁ = t and time₂ = t + 6 months (2 AU), as measured from a nearby star.

From here, it is all simple trigonometry. The star, sun and earth are cornering an imaginary right-angled triangle. By dividing the baseline of 1 AU by the tangent of one arcsecond, or 1/60 arcminute, we get approximately 206 265 AU, or 3.26 light years. This unit of length is called one parallax second, or one parsec. Hence, one parsec can be defined as the distance from which an angle of two arcseconds subtends a body with a diameter of 2 AU.

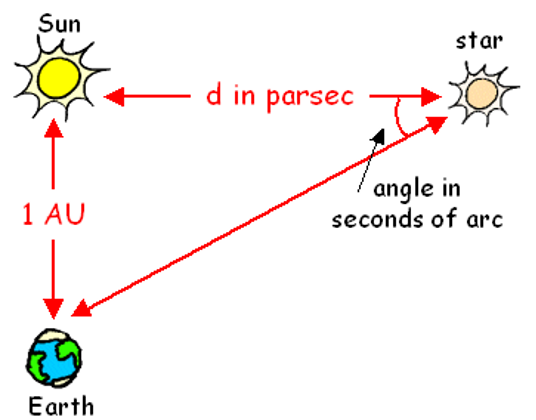
<figcaption>Imaginary triangle formed by earth, sun and some nearby star one parsec away from us. We note one arcsecond as 1”.</figcaption>

However, there are no stars known to us with a distance less than a parsec, hence astronomers have to measure stellar shifts less than one arcsecond. This was impossible before modern technology, but now, ground based telescopes can measure parallaxes as small as 0.01 arcseconds. However, stars beyond 100 parsecs cannot be precisely measured. It was not until we could place telescopes beyond earth’s atmosphere, we were able to accurately measure distances to stars farther away than 100 parsecs. That is because earth’s atmosphere confines the sharpness of the star at which we observe it.

The parallax method is perhaps the most vital calibration step of distance determination in astronomy.